| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
63分6完で39位でした。
atcoder 初参加から、ちょうど半年です。だから何?何もありません。
今回のセットの感想
・F:難しかったけど面白かった!
・E:最近のEにしては易しめ?
・D:最近のDにしては難しめ?
面白かったです。順位も最近の中では高い方でした。
Fで40分。ほとんど詰まらずやり切ったつもりで、割と上出来だと思うのですが、まだまだ最上位には及びませんね。
問題B – 81
9×9に出現する数のsetの作成:
se = set(x*y for x in range(1,10) for y in range(1,10))問題C – Walk on Multiplication Table
$N$ の約数を検出するには、$\sqrt{N}$ まで試し割りすればよいです。こういうのを $10^6$ 回のループを回すと python では遅くなりがちです。単純な並列処理は numpy が簡潔で、コード量も少ないです。
U = 10**6 + 100
x = np.arange(1,U,dtype=np.int64)
div = x[N%x==0]U以下の約数の一覧が手に入ります。$\sqrt{N}$ を上限としてもよいかと思います。定数を上限にするならば、$10^6$ まででよいですが、$1$ 足りない等の処理のミスを予防するために少し余分に計算しています。なお、提出コード実行時間の9割くらいが numpy を import するところにかかっていて、主要の計算部分は 10ms 単位なので、TLEにはまだまだ余裕があります。
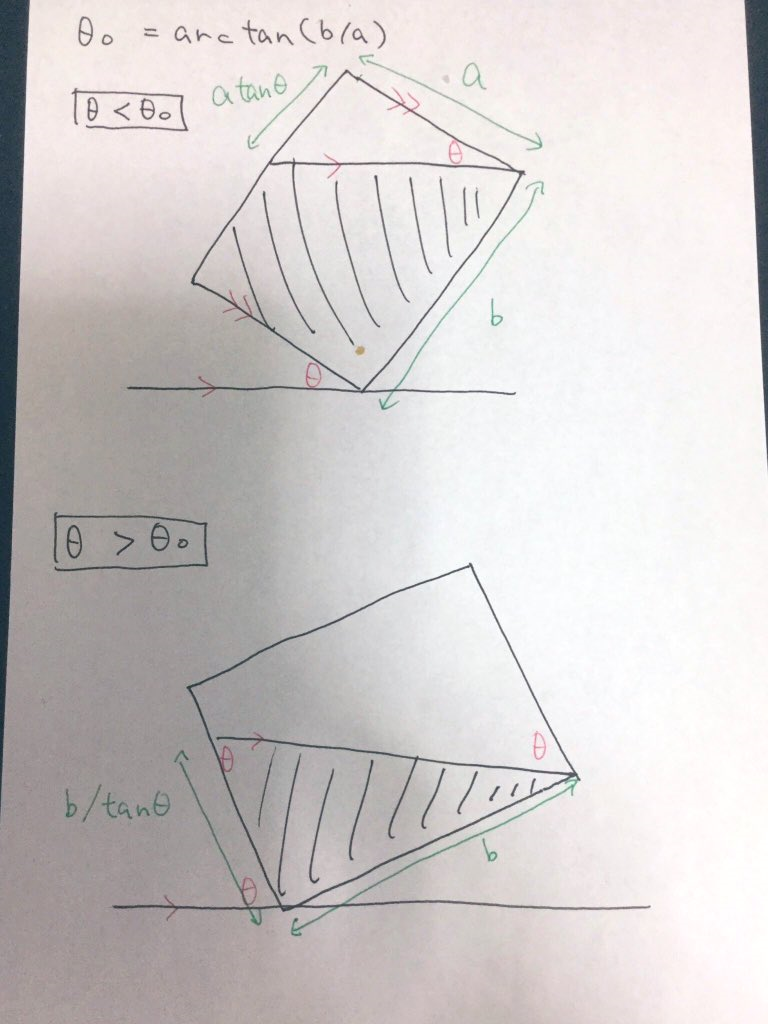
問題D – Water Bottle
基本的な三角関数やそれに基づく立式などは、ある意味、競プロテクニックの大部分よりも世の中で必要とされうる率は高そうで、こういうスキルをきちんと問うていくの非常に良いと思います。
問題E – Gluttony
Asum = A.sum()
def test(x):
# 全員がx秒以下に収めるための必要コストがK以下である
return Asum - np.minimum(A,x//F).sum() <= K問題F – Fork in the Road
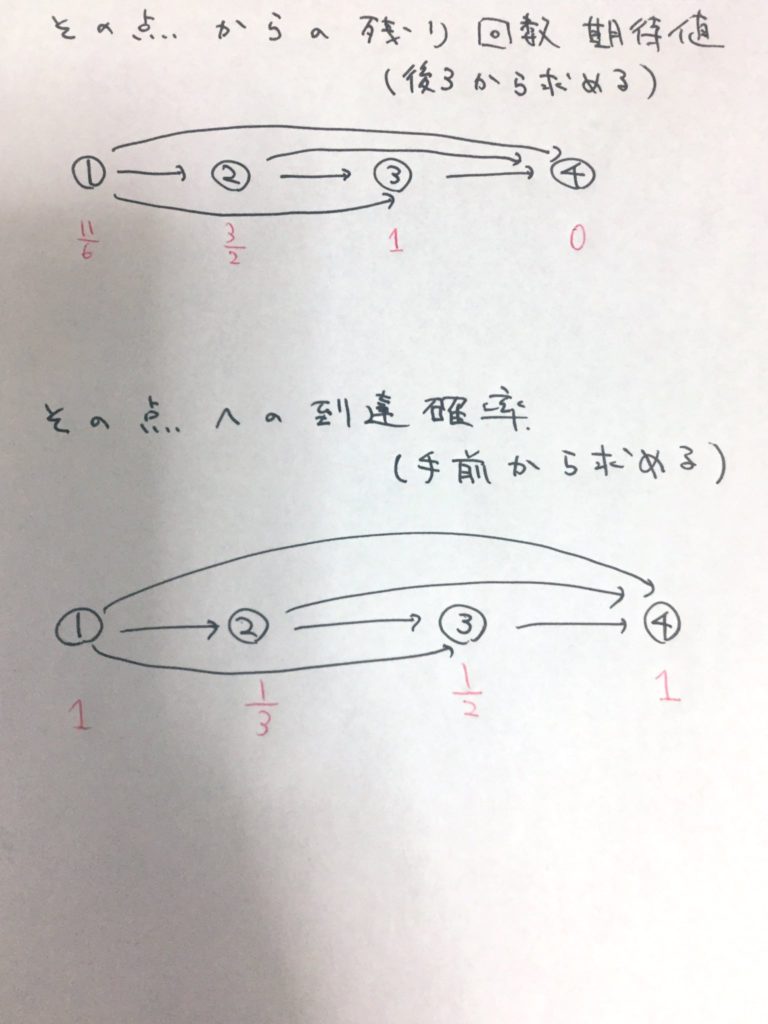
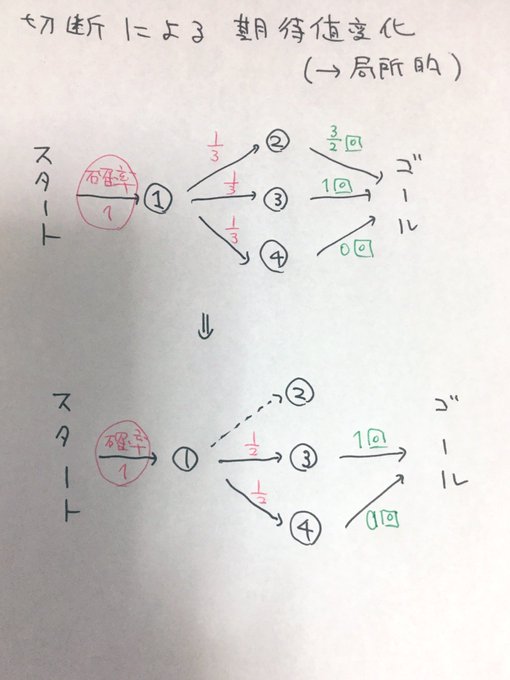
「ループがあったらマルコフ過程で難しいやつだな?」などと少し悩みましたがDAG(directed acyclic graph)に関する問題でした。条件 $s_i < t_i$ が重要です。
1本の辺を切断したとしても、「もともとその辺を通っていた場合」の部分の計算が変更されるのみです。
・辺 $st$ を削除したとする。
・「頂点 $s$ に辿り着かない場合の条件付き期待値」は変化しない。
・「頂点 $s$ に辿り着く場合の条件付き期待値のみが変化する」
ことが分かります。したがって、
・$p = $頂点 $s$ に辿り着く確率
・$x = $頂点 $s$ から出発してからゴールするまでの移動回数期待値(辺削除前)
・$y = $頂点 $s$ から出発してからゴールするまでの移動回数期待値(辺削除後)
としたとき、全体としての移動回数期待値は、$p(y-x)$ だけ変化します。よって、$p,x,y$ が計算できる程度の情報を準備してあげればよいです。これは
・各頂点 $s$ への到達確率(手前から順に計算可能)
・各頂点 $s$ を出発点としたときの、ゴールまでの移動回数期待値(後ろから順に計算可能)
の2つのデータを持つことで達成できます。計算量は $O(N+M)$ です。