| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | |
| 結果 | AC | AC | AC | AC | AC |
全体感想
77分5完(8ペナルティ)で61位でした。
F, Eと開いて、Eはやれば出来そう。Fが苦手っぽいやつ。
Fが方針は立ちそうで、「経験値が少ない・苦手→練習になりそう」と感じたため、Fから着手。
最終的に、Eの方が正解者が少ないというセットだったようです。私はFに長時間を割いたため解ききれませんでしたが、コンテスト後のACは難しくなかったですし、意外です。少なくともFよりはだいぶ易しいと思うのですが。
あと10~20分あれば全完できていたセット。全完だと結構良い順位が出た回だったようなので、ちょっと惜しい。
問題D – Digits Parade
$n$ 桁目までを13で割った余りは、$(n-1)$ 桁目までのそれと、末尾の桁で決まります。
したがって左から順に見て、「そこまで決めた時点で、余りが0, 1, 2, …, 12のものが何通りあるか」を持つ形でdp更新していけます。
(後日)13で割った余りの分布は、何も左から順に更新していく必要はなかったです。例えば、’?’ ではない部分については、最後にまとめてずらすだけです。’?’ については、6桁置きに同じ位置にある ‘?’ は同一視できます。結局、次のようにデータを要約してから計算すればよいです。
・’?’ 以外に書かれた数の寄与
・6k 桁目にある ‘?’ の個数、6k+1桁目にある ‘?’ の個数、…
あとは $\mathbb{Z}/13\mathbb{Z}$ の畳み込みの計算です。同一の数列を何度も畳み込む形になるので、バイナリ法により畳み込みの回数を $O(\log N)$ に減らすことができます。
→ https://atcoder.jp/contests/abc135/submissions/6589145
問題E – Golf
問題Fに時間を費やしたため、コンテスト中には提出できませんでした。コンテスト後に提出した解法について記述しています。
・距離 $2K$ 以内になるまでは、距離が $K$ ずつ減っていくようにする。
・距離 $2K$ 以内とする。偶奇が噛み合うかどうかで、1~3回で決着する。
・この構成で、偶奇が合う範囲内で距離を $K$ 未満しか無駄にしないので、最適。
距離 $2K$ 以内になってからの構成は、偶奇が合わなければ、遠ざからないようにしながら1手パス。したがって、偶奇が噛み合っているときに2手で到達することが本題です。
少し経路を変更すると、目的地を2つずらすことができるので、偶奇が合えば2手で行けるという発想もそれほど難しくないと思います。
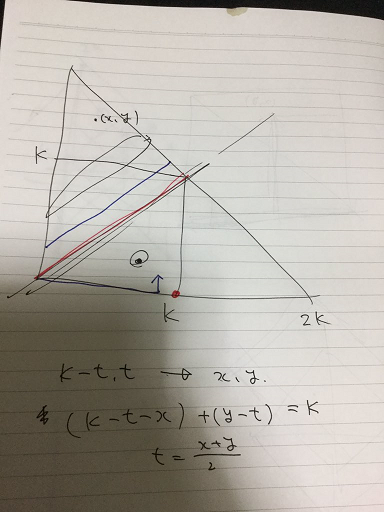
$(K,0)$ に移動すると、2手目に赤線に辿り着けます。ずらして $(K-1,1)$ に移動すると、2手目に青線に辿り着けます。
詳しくは分からないですが、圧倒的な正答率の低さの原因には、実装量があるのではないでしょうか?第1象限・第2象限・…等も気になりますし、上の画像も $x \leq y$ に限定した導出となっています。そこを、場合分けごとの立式をなくしてなるべく頭を使わず済ませられるように実装できれば、普段のABCコンテストE問題と比べて特別高難易度ではないと思います。
提出 → ■ (コンテスト後の提出)
def strategy(x,y,K):
if x < 0:
dx, dy = strategy(-x,y,K)
return -dx, dy
if y < 0:
dx, dy = strategy(x,-y,K)
return dx,-dyこれは、原点から $(x,y)$ に向かうときの1歩目の移動量を求める関数です。
例えばここの部分で、進行方向が第1象限である場合に帰着させています。あとは第1象限にあるときについてのみコーディングすればよいので、実装はそれほど重くならないです。
問題F – Strings of Eternity
とはいえ、ほとんど実装経験値がないので、そこまでスムーズには実装できませんでしたが。
テストケース 1 件あたりせいぜい $10^6$ 回。テストケース $10^3$ 件あっても $10^9$ 回程度しか文字列比較を行わないとします。微小量 $p$ に対して $(1-p)^{1/p}$ が $1/e$ (約37パーセント)に近いことを考えると、$10^{9}$ 回文字列比較を行って全て誤判定しない確率は $(37\%)^{-1/10^7}$ 程度ですので、まず大丈夫かな(競プロじゃない場面でもたいていはほぼ問題にならない?)という値です。
さて、Rolling hash を用いて、$S$ の各場所について、「そこを始点として、文字列 $T$ をひとつとれるか」が判定できます。これができてしまえば、あとはC問題D問題といったレベルの残作業でしょう。
TLE 箇所の確認用 → https://atcoder.jp/contests/abc135/submissions/6576129

