| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
41分全完で、24位でした。
問題Dで答が合わずに5分ほど溶かしていたのが下手でした。問題Fは、過去問の自己提出コードを改変したのですが、どう改変するのかが瞬時に判断できず、結局1からコードを読み直していました。人によっては問題Fはほぼ貼るだけだったかもしれません。
問題E、妙に思考がうろうろして悩みましたが簡単でした。こういうのの反応に時間がかかってしまいますね、うーむ。
公式コンテストの「質問」にデビューしました。全体公開される可能性を踏まえると、もう少し分かりやすい言葉を使う余地があったかもしれません。
問題E – Red and Green Apples
とうぜん美味しさはソートしておきます。赤色、緑色のりんごは $X$ 個、$Y$ 個としてよいです(制約で $X\leqq A$ などが保証されている)。
場合分けの軸を決めます。私ははじめ、使用する赤りんごの個数ごとに、最適解の様子を考えようと思いました。赤りんごの個数を決め打つと、無りんごと緑りんごから適切な個数を貪欲にとることが最適だと分かります。
「無りんご+緑りんご」をソートしておけば、赤りんごの個数を1個減らすたびに、次の候補となるりんごを取り入れることになります。
何となく違和感があります。無りんごと緑りんごを区別せず計算して本当に大丈夫?
検証しても大丈夫そうです。あれれ?緑りんごと無りんごの区別、完全に必要ない??ということは??
くらいで、気づきました。結局、赤・緑の個数を $X$, $Y$ 個に制限してしまいさえすれば、自由に合計 $X+Y$ 個をとって食べることができます。まぜてソートして上位を選んでおわりです。
問題F – Distributing Integers
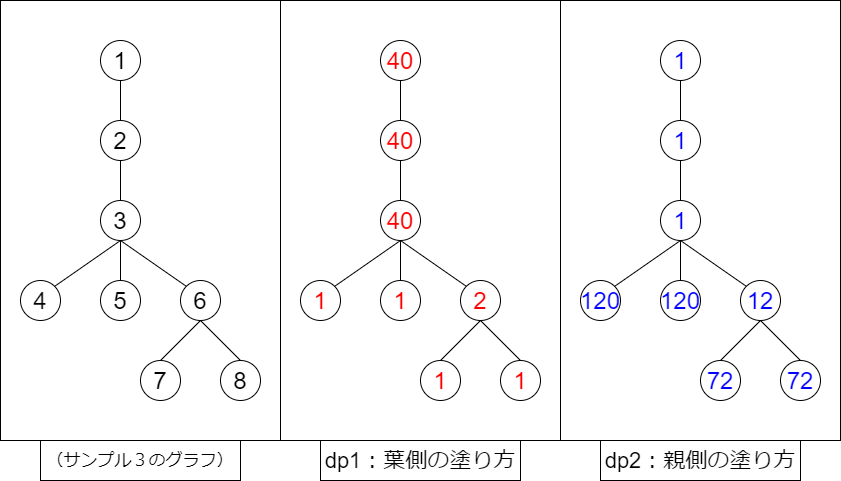
サンプル3のグラフです。まずは、葉側から順に、葉側の塗り方をdpを計算して、そのあと根側から順に、根側の塗り方のdpを計算します。「〇〇側から順に」は、dfsで書いてもよいですし、一度適当なトポロジカル順序を得ておくと、指定の頂点順に for ループをまわすだけになります。
今回は、そもそも数え上げ要素もそこそこ難しいと思います。葉側の値を求める dp の計算は次のような感じです。
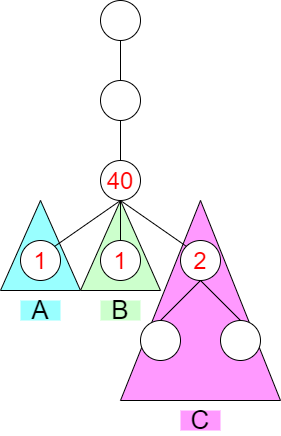
$dp1[3] = 40$ の計算部分です。大きさが $1, 1, 3$ の部分木がぶら下がっていて、それぞれの木の埋め方が $1,1,2$ 通りであるとこれまでの dp で計算されています。これら 5 頂点を埋めるには、まず 5 回の操作を部分木ごとに割り当て(「ABCCC」「ACCBC」など)、そのあとで各部分木の頂点順を決めると考えればよいです。したがって、この場合、$dp1[3] = \frac{5!}{1!1!3!}\cdot (1\cdot 1\cdot 2)$ となります(計算に必要になるため、dp テーブルとともに、部分木の大きさも求めていくことになります)。
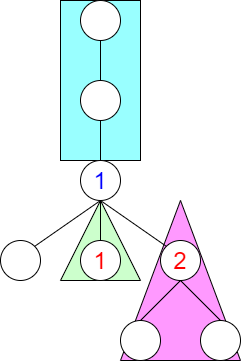
次は、根側の計算です。トポロジカル順序で根に近い頂点から順に計算していきます。ある頂点から根側につながる辺は1つしかないので、まず親を塗ったあとの塗り方が問題です。
親の頂点のまわりに関する計算が必要です。上の図であれば、さっきと同じ要領で、$dp2[4] = \frac{6!}{2!1!3!}\cdot (1\cdot 1\cdot 2) = 120$ と求まりますね。
どの数値に注目してどう計算すればよいかが分かれば、実装は難しくないでしょう。しかし、下手に実装すると計算量が $N^2$ になってしまう恐れがあります。
$n$ 人の子を持つ親が居たとします。子から、親側のdpを計算するとき、$n-1$ 人の子の情報をもらってきたくなりますが、この方法で全頂点に対する計算を行うと、ひとつひとつの子の情報が $n-1$ 回ずつ参照されてしまい、トータルで $O(n^2)$ の計算量になってしまいます。ここの回避の方法は 2 通りあります。以下、$v$ を注目している頂点、$p$ をその親として、
(1)$dp1[p]$, $dp1[v]$ の値から逆算して、$dp1[他の子]$ の寄与を求める。
もともと $dp1[p]$ は、すべての子の $dp1$ の値を掛け合わせて計算されているので、上手く $dp1[v]$ で割るなどすることで、自分以外の子の寄与を計算できます。
(2)左右からの累積を持つことで、数列 $[a_1,a_2,\ldots,a_n]$ から $1$ 要素除いたときの値を全件あわせて $O(n)$ で計算する。
たとえば、 ABC 125:C – GCD on Blackboard に現れている要素です。
今回は、(1)(2)どちらでもよいです(私の提出は(1)になっています)が、(2)でないと上手く書けない問題も存在するので、どちらも覚えておくと良いと思います。
※ dp をマージする部分を上手く抽象化して、ライブラリ化している方もいらっしゃるそうです。私は現状、たいてい 1 から実装してしまっているので、その点については参考にならないです。

