A. Minimal Coprime
$(1,1)$ と $(x,x+1)$ のタイプは coprime であることから長さ $r-l\leq 1$ のものしか考えなくてよいです.$l=r=1$ のときなどに少し注意して数えます.
B. Subsequence Update
$[1,l-1]$ および $[r+1,n]$ 部分のうち,両方を reverse とするものは考えなくてよいです(両端を削る操作を考える).reverse して 2 回解くことにすると,$[r+1,n]$ は無視して解ければよいです.
この場合,$[1,l-1]$ と $[l,r]$ から同じ個数ずつをやり取りすることになります.ソートして累積和を持っておくと,やり取りする個数を決めたときの最適解が計算できます.
C. Remove Exactly Two
操作結果は $n-2$ 頂点の森で,森の連結成分は頂点と辺の個数だけから決まるので,残る辺の個数を最小化する問題になります.
隣接する $2$ 頂点を削除するパターンはすべて計算してしまう.隣接しない $2$ 点を削除するパターンは片方を固定して計算します.隣接頂点の価値を変更してからセグメント木を呼ぶなど.
D. Game With Triangles
上上下ととる回数 $a$,下下上ととる回数 $b$ を考えます.おおよそ次のような問題になります:
- 列 $x=(x_1,x_2,\ldots)$ および $y=(y_1,y_2,\ldots)$ が与えられる(降順ソートされている).$a+b=k, a+2b\leq n, b+2a\leq m$ となる $(a,b)$ を選んで $(x_1+\cdots_x_a)+(y_1+\cdots+y_b)$ を最大化せよ.
適当なタイブレイクで $x_i, y_j$ がすべて異なるとして議論します.
まず,$a+2b,b+2a$ に関する制約を無視した場合には適当な貪欲法が解を与えます.
貪欲法により $k$ 個選んだ場合とは異なる解はどのようなものかというと,これは $a+2b=n$, $b+2a=m$ のどちらかを満たす場合です.$a+2b<n$ かつ $b+2a<m$ であるような解で貪欲解でないものは exchange argument で改善できるからです.
よって貪欲解および $a+2b=n$ や $b+2a=m$ を満たすものを解の候補として最大値を求めればよいです.
E. Triangle Tree
計算すべきは $2\times \min(\mathrm{dist}(u,lca),\mathrm{dist}(v,lca))-1$ の総和です.lca の部分で計算を行うと,$2\times \min(\mathrm{depth}(u),\mathrm{depth}(v))-d-1$ のような値です.
depth の multiset $S$ を何らかの形で管理して, $\sum_{x\in S}\min(x,a)$ のようなクエリと $S$ への値の追加が行えればよいです.DSU on Tree のように heavy path ごとに計算すると,大きさ $O(N)$ のデータ構造をリセットして使いまわせるので実装しやすいと思います.
F2. Counting Is Not Fun (Hard Version)
まず最終的なかっこ列を木構造で表します.両端に (, ) を追加しておくと,(森ではなく)すべての頂点がペアであるような根付き木になるので少し考えやすいかもしれません.
設定ではペアが順にわかっていくという順ですが,逆順に処理することでペアがだんだん分からなくなっていくという問題だと考えます.
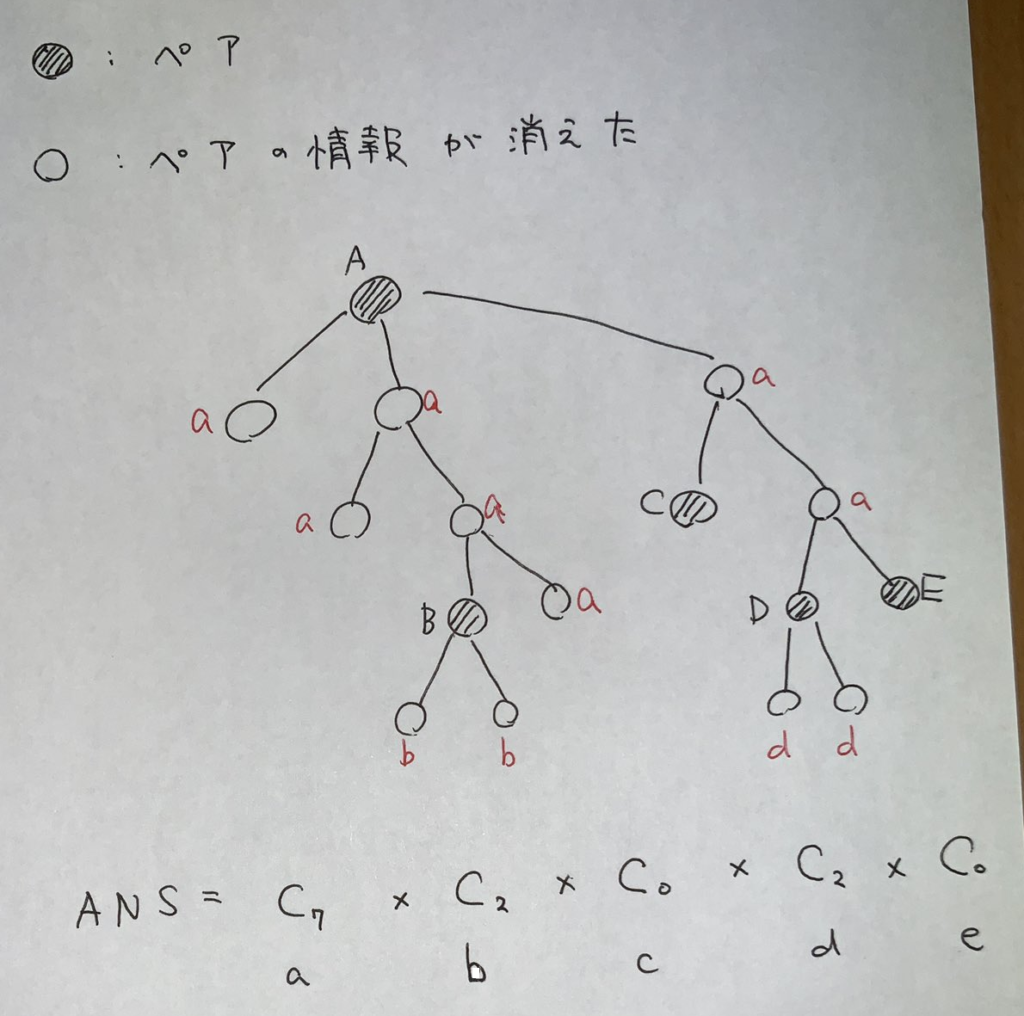
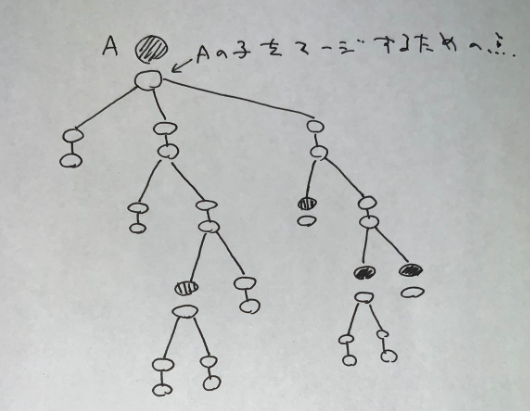
このとき答はどうなるかというと,ペア情報が消えた頂点を,その最も近い先祖のでペア情報がある頂点で分類し,各同値類について対応するカタラン数を掛け合わせるという形になります.あとはペア情報を消しながらこのような計算を行えばよいです.
ある頂点と子をマージしたくはないが,子はマージされるようにしたい.というような状況が発生します.各頂点について子をマージするための頂点を追加するような頂点倍化をしておくと,グラフの $O(N)$ 個の辺についてのマージクエリとして処理できます.