概要
本記事では,次の問題たちの関連を述べます.(出題時期順のつもりですが間違ってるかも.)
- [Icy Roads Of Nomel], Gennady Korotkevich Contest 1.
- [01 on Tree], AGC023.
- [Heavy Stones], Yuhao Du Contest 7.
- [京都観光], JOI 2022 春合宿, 実は [Icy Roads Of Nomel] と完全に同じ.
- [Train Seats], NPCAPC 2024, 実は [Heavy Stones] とだいたい同じ.
この記事ではどの問題の解法も完全には説明していませんが,いくらかのネタバレは含まれています.
[京都観光] の [01 on Tree] への帰着
行(横線)・列(縦線)の個数を $1+H, 1+W$ として,各行・列の重みを $a_i, b_j$ と書くことにします.
$i$ 行目の到達を $A_i$, $j$ 列目の $B_j$ と書くことにすると,グリッドパスは $H+W$ 個のもの $A_i, B_j$ ($1\leq i\leq H$, $1\leq j\leq W$) の並べ替えに変換できます.ただし,「$i<j$ ならば $A_i$ よりも $A_j$, $B_i$ よりも $B_j$ の方が右側に来る」という条件がつきます.
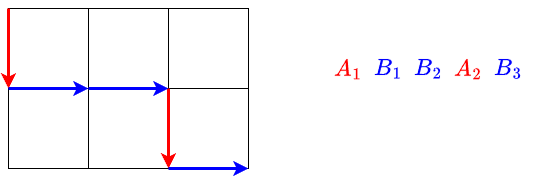
各行の寄与を考えてみると,次のようになります.$i=0,H$ まわりは適切に欠損値を定義する必要がありますが,この議論は省略します.
$A_i$ により右にある $B_j$ の個数を $x_i$ とするとき,$a_i$ は $x_i-x_{i+1}$ 回加算される.
行の寄与の総和は $\sum a_i(x_i-x_{i+1})=\sum (a_i-a_{i-1})x_i$ となります.
改めて $p_i=a_i-a_{i-1}$ とおき,$i=0,H$ まわりを適切に処理すると,行の寄与の総和を $c+\sum_{i=1}^{H} p_ix_i$ という形に書き直すことができます.
列についても同様の処理をするとで,本問を次のような転倒数の問題へと書き換えることができます:
$H+W$ 個の 01 文字列 $A_i, B_j$ がある.各 $A_i, B_j$ は次のような形である:$100\cdots 0$($1$ に $0$ を $p$ 個付ける).これらを「$i<j$ ならば $A_i$ よりも $A_j$, $B_i$ よりも $B_j$ の方が右側に来る」という条件が成り立つように並べるとき,できる文字列の転倒数を最小化せよ.
個人的には転倒数の問題と解釈するのが分かりやすいと思ったのでそのようにしましたが,$p$ は負にもなってしまう(辺重みが実数という設定ならば実数にもなる)のでこのままでは変です.受け入れにくい方は意味を汲み取って適切に定式化しなおしてください.例えば文字 $0$ に重み $p$ をつけた転倒数と思えばよいです.
また,実際には求めるべき値は,できる文字列の転倒数ではなく,そこから $A_i$ 由来の文字同士・$B_j$ 由来の文字同士の転倒数を引いたものなのですが,$A$ 同士・$B$ 同士の順番は決まっているのでこのような書き換えができます.
$A$ 同士・$B$ 同士では順番が決まっているというのは,次のような根付き木でトポロジカル順を保って文字列を結合するというのと同じことです.
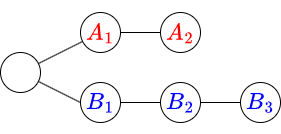
よって,[京都観光] は [01 on Tree] と同様の方法で解くことができます.この解法については省略します.(先に述べた $p<0$ になりうることも解法に影響しないことが確認できます).
[Train Seats] の [01 on Tree] への帰着
最初私は [Train Seats] から [京都観光] への帰着を一度経由したのですが,直接 [01 on Tree] にした方が簡単でした.
[Train Seats] はすぐに [Heavy Stones] に帰着できるので,こっちを解説します.これはやっぱり,次のような根付き木から 01 文字列をとっていったときの転倒数最小化という問題に帰着できます.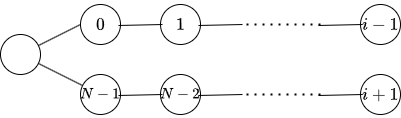
よってこれも同じように解くことができます.
$i$ によって木の形が変わるため少し実装量が増えますが,01 on Tree の計算を十分理解していれば残りの解法の導出は難しくないと思います.
- 解答例 (Heavy Stones):https://qoj.ac/submission/621998
- 解答例 (Train Seats): https://atcoder.jp/contests/npcapc_2024/submissions/58564666

