参考文献
- Elegia さん:https://codeforces.com/blog/entry/92183
- 本記事で扱っているアルゴリズムはここで紹介されているものとほぼ同一です.ただし以下の点について,定式化や議論を変更・追加しています.
- 分母 $\frac{1}{k!}$ について説明し,EGF との合成が任意の環で定義できることを確かめた.それに応じて計算方法の導出も変更した.
- 多項式との合成を EGF との合成に帰着する議論(簡単)について述べた.
- 本記事で扱っているアルゴリズムはここで紹介されているものとほぼ同一です.ただし以下の点について,定式化や議論を変更・追加しています.
- Library Checker
EGF との合成(問題の定式化)
$K$ の元の列 $f_0, f_1, \ldots$ に対して,次の形の式を $f$ の指数型母関数(EGF, exponential generating function)といいます:
$$f(x) = \sum_{k=0}^{\infty} f_k\frac{x^k}{k!}$$
$f$ は集合べき級数ではなく形式的べき級数であることに注意してください.
$a \in K^{2^n}$ の定数項が $0$ であるとき,$f(a) = \sum_{k=0}^{\infty} f_k\frac{a^k}{k!} \in K^{2^n}$ を求める問題を考えます.なお,$[x^0]a=0$ という制約のもと,$k > n$ に対して $a^k=0$ となるので,実際には有限和 $\sum_{k=0}^n$ を考えれば十分です.
この記事では $K$ が環であるとして集合べき級数の定式化をしています.そのため,$f(a)$ の定義は有限和 $\sum_{k=0}^n$ とした場合でも,まだ不十分で,$k!$ が乗法逆元を持つ保証がないという点に対処する必要があります.
非負整数 $k$ と集合べき級数 $a$ に対して,$\frac{a^k}{k!}$ に相当するものをうまく定義できます.$a_0 = 0$ を用いると,集合 $s$ に対して,$[x^s]a^k$ は次のように表すことができます:
- $[x^s]a^k$ は,$s$ の空でない集合への分割 $s = \coprod_{i=1}^{k}t_i$ をわたる $\prod_{i}a_{t_i}$ の和である.
このような集合への分割において,$i\neq j$ ならば $t_i\neq t_j$ が成り立つことに注意してください.($t_i\cap t_j = \emptyset$ と $t_i\neq \emptyset$ から分かります.)
このことから,ひとつの分割から添字を並べ替えることで得られる $k!$ 個の分割はすべて異なり,$[x^s]a^k$ は同じ値を $k!$ 個ずつ足す形で表せることになります.よって添字を入れ替えただけの分割を 1 度しか足さないように修正して上で述べた計算を行ったものとして,$\frac{a^k}{k!}$ を定義することができます.例えば次のように表すことができます.
- $[x^s]\frac{a^k}{k!}$ は,$s$ の空でない集合への分割 $s = \coprod_{i=1}^{k}t_i$ (ただし $t_1 < \cdots < t_k$)をわたる $\prod_{i}a_{t_i}$ の和である.
以上により $\frac{a^k}{k!}$ を定義することができました.(誤解を招きやすい記号を用いていますが,集合べき級数を $k!$ で割るという操作は定義しておらず,$\frac{a^k}{k!}$ という集合べき級数のみを定義しています.)
EGF との合成の計算
指数型母関数 $f(x) = \sum_{k=0}^{\infty}f_k\frac{x^k}{k!}$ と集合べき級数 $a$ (ただし $[x^0]a=0$ )に対して $f(a)$ を $\Theta(n^22^n)$ 時間で計算する方法について述べます.
$0\leq d\leq n$ に対して指数型母関数 $f^{(d)}$ を $f^{(d)}(x) = \sum_{k=0}^{\infty} f_{k+d}\frac{x^k}{k!}$ により定めます.(なお,$d$ 階導関数の記号と整合的な記号です.)
計算手順は次の図で表すことができます.図では $n=3$ としています.
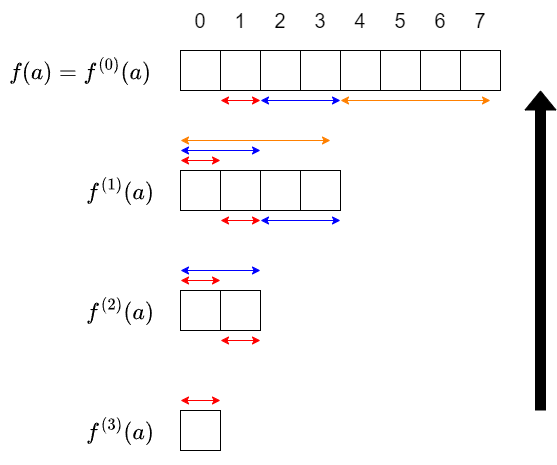
$f^{(d)}(a)$ の先頭 $2^{n-d}$ 項を求める問題を,$d=n$ から降順に解いていきます.
簡単のため $f^{(1)}(a)$ から $f^{(0)}(a)$ を求める部分のみ解説します(他の部分も同様です).図では次で表される部分です.
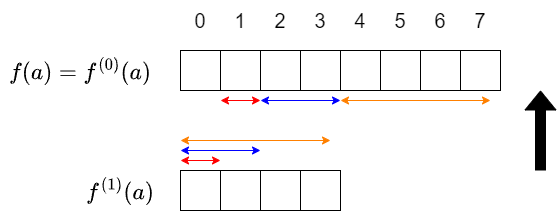
まず,$k>0$ に対して $\frac{a^k}{k!}$ の定数項は $0$ なので,$f(a)$ の定数項は $f$ の定数項 $f_0$ が入ります.そこから先は次の手順で計算します:
- $f^{(1)}(a)$ の $0$ 項目を用いて,$f(a)$ の $1$ 項目を計算する.
- $f^{(1)}(a)$ の $0, 1$ 項目を用いて,$f(a)$ の $2, 3$ 項目を計算する.
- $f^{(1)}(a)$ の $0, 1, 2, 3$ 項目を用いて,$f(a)$ の $4, 5, 6, 7$ 項目を計算する.
$f^{(1)}(a)$ の先頭 $2^m$ 項から,$f(a)$ の $2^m$ 項目から $2^{m+1}-1$ 項目までを計算する方法を説明します.
$2^m\leq s < 2^{m+1}$ に対して,$\frac{a^k}{k!}$ の第 $s$ 項は次のように書けるのでした.
- $s$ を $k$ 個の部分集合 $t_1, \ldots, t_k$ ($t_1 < \cdots < t_k$) に分割する方法を考える.
- $[x^s]\frac{a^k}{k!}$ は,そのようなすべての分割 $(t_1, \ldots, t_k)$ に対する $\prod_i a_{t_i}$ の和である.
ここで,$m\in s$ なので,このような組に対して $m\in t_k$ が成り立ちます.$(t_1, \ldots, t_{k-1})$ は $s-t_k$ の空でない $k-1$ 個の部分集合への分割です.このとこから,
$$[x^s]\frac{a^k}{k!} = \sum_{m\in t, t\subset s} [x^{s-t}]\frac{a^{k-1}}{(k-1)!}\cdot [x^{t}]a$$
が分かります.これは,subset convolution と非常によく似ており実際,$s, t$ の代わりに $s’ = s-\{m\}$, $t’ = t-\{m\}$ を考えることで右辺は $\frac{a^{k-1}}{(k-1)!}$ と $a$ のスライスの subset convolution として表すことができます.
$f_k$ 倍して $k$ について和をとることで,次の計算方法が得られます.
- $f^{(1)}(a)$ の先頭 $2^m$ 項と,$a$ の $2^m$ 項目から $2^{m+1}-1$ 項目の subset convolution が,$f(a)$ の $2^m$ 項目から $2^{m+1}-1$ 項目までと一致する.
以上を適切に実装すれば,$f(a)$ を計算することができます.
全体の計算量は $\Theta(n^22^n)$ 時間となります.計算量解析は,簡単にいえば,全体を通して $2^{n+1}-1$ 個(上の図のマスの個数)の値を計算することと,ひとつの値あたり平均 $O(n^2)$ 時間の計算量であることから確かめられます.
実装の定数倍など
- $d$ を降順に計算すれば,よくある dp テーブルの次元削減テクニックが使えます.つまり $d$ ごとの $1$ 次元配列(全体で $2$ 次元配列)を用意せずとも, $2$ つの $1$ 次元配列で事足ります.ただし使う列の長さが指数的に長くなるため,一般的な $2$ 次元配列上の dp の場合と比べて恩恵は少ないと考えられます.
- $a$ の同じ部分を繰り返し subset convolution に用いるため,同じ列のランク付きゼータ変換が複数回必要になります.これを 1 度しか使わないことでも定数倍改善が可能ですが,https://judge.yosupo.jp/problem/polynomial_composite_set_power_series で実装した限りでは,やはり恩恵は大きくはないように見えます.
exp との合成の計算
$f(x) = \exp x = \sum_{k=0}^{\infty} \frac{x^k}{k!}$ とします.つまりすべての $k$ に対して $f_k = 1$ である場合の $f(a) = \exp a$ の計算を考えます.
この場合には任意の $d$ に対して $f^{(d)} = f$ であることを利用できて,より実装,計算量の定数倍が軽いです.
多項式との合成の計算
$f(x) = \sum_{k=0}^d f_kx^k$ を多項式とし,$a$ を集合べき級数($[x^0]a = 0$ とは限らない)とします.
$[x^0]a \neq 0$ より $a^n\neq 0$ は成り立たないことに注意してください.したがって $k>n$ の係数も結果に影響します.また,形式的べき級数と集合べき級数の合成は一般的には考えられません.
$f(a)$ を計算する問題は,次のようにして EGF と集合べき級数の合成に帰着できます:
$c = [x^0]a$ とします.$g(x) = f(x+c)$ により多項式 $g$ を定めると,$g(a-c) = f(a)$ です.$[x^0](a-c) = 0$ なので,$g$ を EGF として表して $a-c$ に代入すれば,上で解説したアルゴリズムが適用できます.
$g(x)$ の計算は $f(x+c)$ とすると Polynomial Taylor Shift の計算になりますが,$g$ を $n$ 次まで計算すれば十分であることから,各 $k$ に対して $(x+c)^k$ の $n$ 次までだけを計算することで $O(nd)$ 時間で計算できます.
あるいは多項式の Taylor 展開 $f(c+x) = \sum_{k=0}^{\infty}f^{(k)}(c)\frac{x^k}{k!}$ を利用すると,$f^{(k)}(c)$ が $f(c+x)$ の EGF の係数を与えることが分かるので,これを計算すると考えてもよいです.

