進捗
650問 → 675問

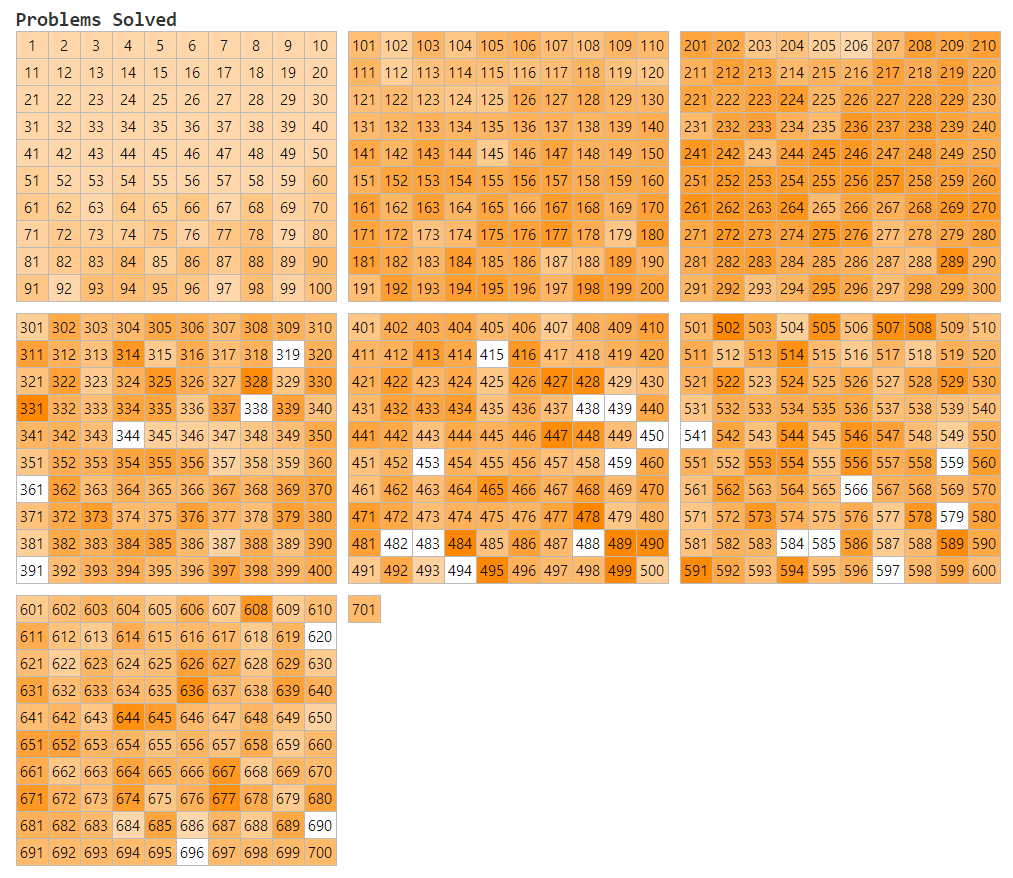
650 / 677 → 675 / 700.
新しい問題を9割方クリアしつつ、いくつか個人的未解決問題も解決できて、未解決問題数が減っているのが嬉しいところです。プレイするコンテンツ数を増やしていてなかなか上手く両立できていないですが、引き続き最高レベル帯を維持していけるといいかなと思っています。
久しぶりにやると、Eulerもとても楽しいですね。他の競技プログラミングと比べると、環境の制約が何もない分、色々なライブラリ、JITコンパイルや並列処理などの高速化など、自由にいろんなことを学べるのも良いところです。
また、AtCoderで易しい問題を十分量練習したおかげもあってか、以前と比べて実装で悩むことや、バグらせて時間を溶かすことが少なく進められているような気がします。
感想など
・[689] 好き問題です。確率分布に関する適切な理論を使うと鮮やかにまとまります。緩く確率論をやるだけでも答を出すには十分です。
・[697] この問題も確率分布を頑張っていじいじしましたが、簡単な計算結果が出てきました。よく考えたら当然という。
・[514] 昔はピックの公式に基づいて考察して行き詰まっていました。AtCoderの問題を考えていたときの経験で上手く計算できました。
・[484] 難易度100%がついているわりには易しかったです。 えー、てか過去の私、計算量を落とすどころか考察の序盤すら抜けられていなかったの、なぜ。
・[699] 7着。既存の書き込みが、自明でない事実を言及なしに仮定しているように見えたので、その辺の事情をより明示する形でthreadへの書き込みをしておきました。
・[427] シンプルな難問。$N^2$で解けるのは分かっていたけど、あとはちゃんと式を作って変形する。
・[478] これは難しい。射影平面よく分からなくて計算がつらそう、というところで止まっていた。よく考えたらそこの言い換えは簡単にできて、多項式時間で計算できそうな感じにはなる。でもそこからも難しかった。類題はあるのだけど。バグらず一発で答が合ってうれしい。
・[695] 割と好き。膨大な入力データを上手くさばくというのが競プロでの典型という印象がありますが、Eulerでは、定義がシンプルで大量なデータも含まないような図形の計量、確率・期待値の計算が問われることも多く、そういうの好きですね。ちょっと6次元空間とか考える気がしないと思っていましたが、何と何が独立かを丁寧に考えると、上手く計算できました。

