A. Did We Get Everything Covered?
最初の出現が一番遅い文字を $1$ 文字目に置く,というタイプの貪欲をします.
B. Space Harbour
ほぼただの実装問題です.港の間に挟まれた部分の和をセグメント木などで持ち,クエリ区間の両端を含む部分は都度計算します.
C. Fractal Origami
線形漸化式の形になります.
D. Balanced Subsequences
カッコ列を例の累積和によって,$(0,M)$ から $(0,N)$ までの折れ線と対応させます.
すると,通る点の $y$ 座標最小値が $K$ だという条件になります.
「$y=K-1$ を通らないもの」から「$y=K$ を通らないもの」を引けばよく,それぞれ鏡像原理で求まります.
E. Paper Cutting Again
操作回数は,すべての状態に対して「その状態から操作をする回数」を足したものです.
よって未終了であるようなすべての状態に対して,「その状態への到達確率」を足したものです.
到達確率は,次のように考えると分かりやすいかもしれません.操作は「まだ残っている縦線・横線から選びカットする」ことですが,これを「最初に存在するすべての縦線・横線の順列を選び,その順に線を選んでいく(ある線がすでに消えてたら操作は無視)」とします.
すると各状態への到達確率は,順列のうちである要素がこれらの要素の手前に現れるもの,というタイプの確率として表され,計算できます.
これで $O(NM)$ 時間の解法になりますが,累積和などを使って高速化できます.
F. Anti-Proxy Attendance
まず $N=3$ が解ける必要があります.さらに,$N=3$ の解法があると,要素を $3$ 分割して同じようにすれば候補となる $2$ グループを検出することができるので,$O(\log N)$ クエリで解くことはできます.結局定数倍を無視すれば,$N=3$ に帰着できるので,$O(\log N)$ クエリで解くだけならば簡単だということになります.
実際に次のような戦略が可能です.
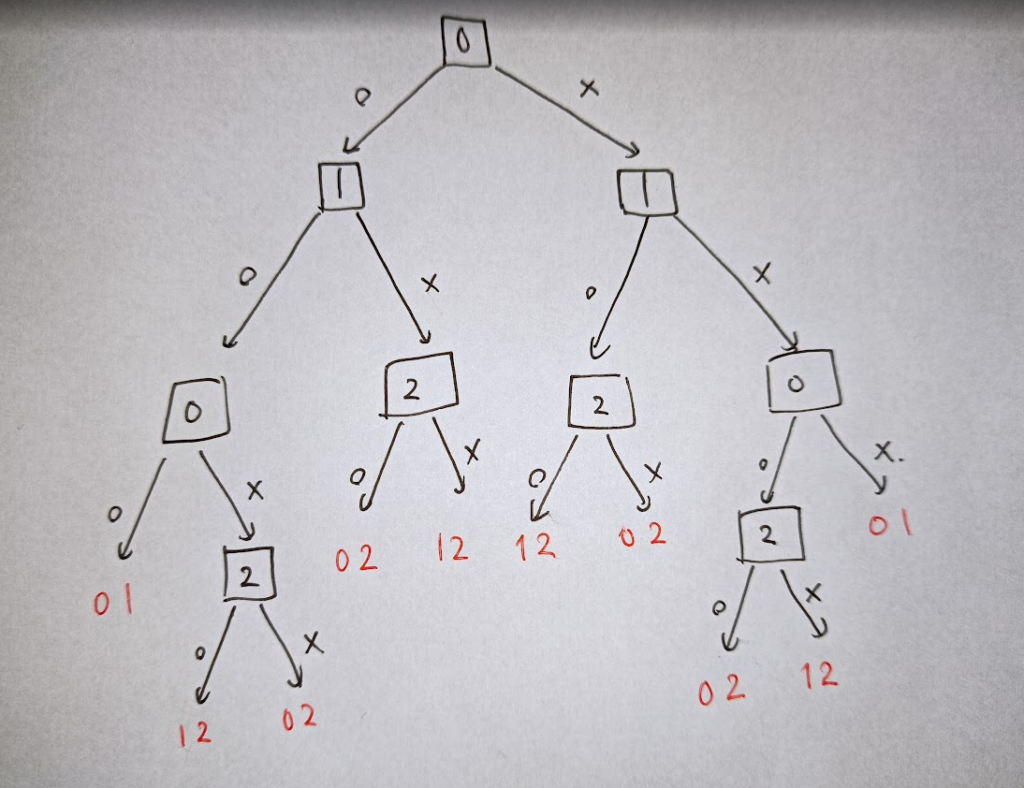
$3$ 元集合に対して $4$ 回以下で候補を $2$ 元集合に絞っていますが,「$4$ 回で $2/3$ 倍になる」という規則ではクエリ回数が足りません.
このとき,「$4$ 回かかるのは $\{0,2\}$, $\{1,2\}$ のどちらかの場合」であることに注目します.集合 $S$ が与えられたとき,$S$ を $S_0,S_1,S_2$ に分割しますが,$S_2$ に比べて $S_0,S_1$ が少し大きくなるような分割します.$3$ 回で候補が減る場合の要素数を増やす代わりに $4$ 回かかってしまう場合の要素数をより大幅に減らせるように調整します.
$k$ 回以内に解けるような最大の $N$ を $\mathrm{dp}[k]$ として最適化できます.
線形漸化式を見ることで,漸近的には $N=O(x^k)$ ただし $x$ は $x^4=\frac12 x+1$ の解ということになっていて,これは $1.1173\cdots$ で問題文の設定に合っています.

