A2. Make Nonzero Sum (hard version)
総和が偶数であることが必要です.十分条件にもなります.$0$ を除去してから考えると,長さ $2$ の $\pm 1$ 列に対処すればよく,長さ 2 でとるか長さ 1, 1 でとるかすればよいです.
B. Factorial Divisibility
$a_i\geq x$ となるものは無視できます.昇順に見て,$a_i=k$ が $k$ 個あればこれを $1$ 個の $k+1$ に置き換えて構いません.$k<x$ でこれができなかったら総和が $(k+1)!$ でないことが分かるので不可能です.
C. Wish I Knew How to Sort
$0, 1$ の個数を $a,b$ とすると,状態として,「左 $a$ 個のうちにある $1$ の個数」(これは右 $b$ 個のうちにある $0$ の個数)だけに注目すると簡単に計算できます.
D. The Beach
解法は,空マスの移動をグラフになおして最短路問題を解くというものです.
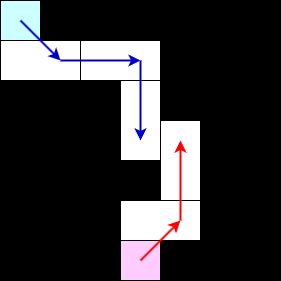
グラフの構築の際には,現在のタイルの配置だけを考えることにして,空マスとタイルの隣接があるき,タイルとタイルの隣接関係があるときに上手く辺を張ります.
空マスは parity によって 2 種に分類できて,このグラフにおいて 2 種の空マスが隣接するための最小コストが答になるというものです.
一方で,これが答になるというのはあまり自明ではないと思います.タイルの位置が変化することによって新しい操作が生じて答に影響する可能性を否定するのはあまり簡単ではないと思います.解説では
It can be shown that in the optimal answer we use no more than one operation with each sunbed.
と書かれていますが,証明が書かれておらず,コメント欄で議論になっていました.
私も結構悩んだのですが,最終的には次のように証明するのが明快かなと思いました.
タイルの配置 $X$ に対して,$f(X)$ を想定解法の与える最小コストとします.コスト $p$ の操作によって $X$ が $Y$ に変化したとするとき,$f(X)\leq f(Y)+p$ を示せばよいです.$f(X)=0$ の場合は自明で,そうでないとき $X, Y$ のグラフは局所的に辺を少し張り替えただけになっており,これは比較的簡単に証明できます.
E. N Machines
$1$ をかける操作は無視すると,掛け算は $30$ 回程度までしか登場しません.
掛け算については先頭に,加算については末尾にうつすのが最適です.
末尾にうつす掛け算の個数を決めてしまうと,各足し算を先頭に移動させる利得が決まり,価値の高いものから決まった個数をうつす貪欲法が正当です.これは掛け算で区切られた区間ごとにソートして累積和等を持っておけば,適当な polylog 時間で解けます.
これで,例えば $2^{30}$ 通りについて polylog 時間の計算をすれば解けるということになります.
これはまだ多すぎるのですが,次の枝狩りが有効です:先頭から見て $a$ 倍を末尾に移さなかったら,それ以降 $a$ 倍以下であるものを末尾にうつすことはない.
これをやると,考えるべき掛け算の移動方法が非常に少なくなり,解説によれば制約内で最大 $4600$ 通り程度であるようです.
F. Minecraft Series
正方形のスコアは,正の部分の mex と負の部分の mex の和です.
$ans[i][j]$ を,$(i,j)$ を左上端とする正方形で目標達成できる最小の正方形サイズとします.
$ans[i][j]-1\leq ans[i][j+1]$ などが示せるので,適当な尺取り法をすれば,正方形の一辺の拡張・縮小を合計 $O(NM)$ 回程度で解くことができます.一辺の拡張や縮小のために $O(\min(N,M))$ 個のマスを参照するので,$O(NM(N+M))$ 回,1 マスの追加・削除を行えば解けそうです.
しかし,$K$ 個のデータが一様に分布しているわけではないので,似た解法でも計算量が悪くなってしまうパターンがあります.例えば $i$ を固定して $j$ をインクリメントしていくことを考えます.このとき
$$[0,n]\times [0,n]\to [0,n-1] \times [1,n] \to [0,n]\times [1,n+1] \to [0,n-1]\times [2,n+1]\to [0,n]\times [2,n+2]\to\cdots$$
のような追加・削除が行われると,マス $(n,n)$ が $n$ 回参照されます.これを各行でやるとひとつのマスが $\Omega(\min(N,M)^2)$ 回参照されてしまうということが起こり得ます.
正しい尺取りの方法は,対角方向に進めるというものです.$[i,i+n]\times [j,j+n]$ から先頭を pop して $[i+1,i+n,j+1,j+n]$ に進んだとき,この pop された要素が対角方向に進む一連の操作で二度と push されないというのが上述の尺取りとの違いになります.
あとは,多重集合への追加と mex クエリをある程度高速にさばければよいということになります.例えば bitset を使って追加を $O(1)$ 時間で行い,mex クエリを $O(K/w)$ 時間で行うことで AC できます.mex クエリに比べて追加の方が大量に来るので追加の速度を優先すると良いです.
なお平方分割で追加 $O(1)$,mex クエリ $O(\sqrt{K}/w)$ というのも実装しましたが,追加の定数倍が少し増えるためこっちの方が実行時間が長くなりました.
定数倍について少し調べましたが,行や列方向に連続したマスに入っている値をメモリ効率良く手に入れられるようにするような実装は,あまり定数倍には利かず.各マスに入っている値をソートしておく(解説に書かれている)アイデアは結構利きました.

