A. Competitive Programmer
総和が $3$ の倍数で,末尾 $2$ 文字を「偶数・0」とできる場合です.
B. Dice Tower
最上段以外は $14$ ずつ加算されます.最上段の総和は $6$ 通りあります.
C. Diverse Matrix
(1,1) の場合は不可能です.それ以外は $H+W$ が達成可能です.
各行,各列の値をそれぞれ適当な連番にしたあと各マスに積を書き込んでいくと,基本的には条件達成です.gcd の上界として $2$ 数の差がとれるため,連番が有効です.ただし行数または列数が $1$ の場合の処理に気を付ける必要があります.
D. Decreasing Debts
各頂点の流出量と流入量の差分が不変です.差分が正のところと負のところを適当にマッチさせていきます.
E. Spaceship Solitaire
すべての bonus が発動したと仮定した場合に $i$ が受け取れる量を $b_i$ とすると,$i$ に対する操作は少なくとも $\max(a_i-b_i,0)$ 以上必要です.
なんと実はこれが達成できます.同じ $(s,t)$ がひとつ以下しかないことが利いています.
$\max(a_i-b_i,0)$ ずつ自分で操作したあと,可能な限り bonus をすべて発動した状態を考えます.完成した $i$ は無視して,未完成の $i$ が残っているとします.現在の到達度を $x_i<a_i$ とします.今後 $i$ を始点とする bonus は高々 $a_i-x_i-1$ 個しかありません.未完成の $i$ がひとつ以上あるとき $\sum (a_i-x_i-1) < \sum (a_i-x_i)$ なので,ここからすべての bonus を発動してもすべてが完成することはなく,矛盾です.
F. Almost Same Distance
選ばれる点集合の中心をとると,「各部分木方向からおおよそ同じ深さの点を選ぶ」という感じの条件になります.よって各有向辺ごとに,部分木方向の深さを前計算しておきます.
中心が頂点の場合は,比較的簡単に処理できます.次数に比例する計算量を使っても線形時間です.
中心が辺の場合が少し大変です.中心を $2$ 点集合だと思います.
「各部分木方向」と先ほど書きましたが,このときには中心の隣から見て各部分木方向ということになります.両者の次数の max に比例する計算量を使っていては star に近い構造のときに計算量が $\Omega(N^2)$ になってしまいます.
次数が大きい点については,その点に関する前計算を行い,次数の近傍との辺を結ぶ場合をそれぞれ計算していくようにすると,計算量を $O(N^{1.5})$ にすることができます.
G. Permutation Concatenation
実験エスパーのみで攻略成功.LCP array における各値の頻度を求めて調べます.2 次元テーブルに出力して斜めの比を見たりすると上手くいきました.
解説は少し読んだけど,証明されていない場所があるように思い,あまり面白そうではなかったので理解をあきらめ.
H. Red-Blue Graph
特に前計算はせず,クエリごとに独立に解きます.
各頂点・辺を通る回数の決定(必要条件 1)
$v$ から出る赤辺を通る回数を $x_v$ とします.$v$ から出る青辺を通る回数は $x_v$ または $x_v+1$ で,入力文字列 $s$ から決まります.
辺の状態が同じときに同じ頂点を $2$ 回訪れるとするとループに入っていて特に頂点 $n$ を通っているはずです.よってこれは除外できて,$0\leq x_v \leq 2^n$ が分かります.
各頂点への流入量・流出量を考えることで,$x_v$ に関する連立 $1$ 次方程式が出てきて,$n\times n$ 行列 $A$ と列ベクトル $b$ について $Ax=b$ と表されます.
この行列 $A$ は,有向グラフのラプラシアン行列です.第 $n$ 行,第 $n$ 列を除いたものは行列式が $n$ を根とする有向木の個数と等しいです.頂点 $n$ に到達可能という仮定からこの行列式は正で,また明らかに $2^n$ 以下です.
よって素数 $p$ を $p>2^n$ を満たすようにとって,mod $p$ で連立方程式を解くことで,$(x_v)_v$ の候補を高々ひとつ復元できます.この候補において流入・流出量が釣り合っているというのが解の必要条件となります.
反例
必要条件 1 は十分条件にはならないです.サンプルに反例があります.
4 BRBBR
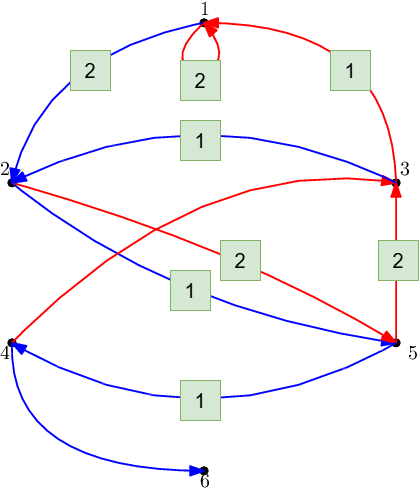
上のように有向辺の回数を定めると,最終的な各頂点の色や流入・流出量は矛盾しません.が,実際にシミュレーションすると次の状態で頂点 $4$ に到達します.
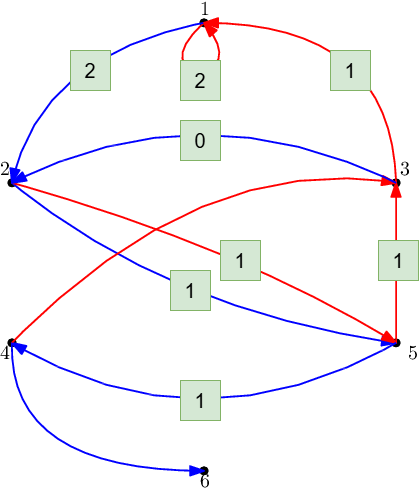
必要条件 2
各頂点から出る辺のうち,最後に通った辺だけを残してできるグラフを考えます.より正確には
- $v$ を通ったことがない場合:出る辺は存在しない
- $v$ が最後に訪れた頂点である場合:出る辺は存在しない
- それ以外:$v$ から最後に出た辺を張る
とします.すると,次が証明可能です:訪れたことがない頂点を除くと,上のグラフは $v$ を根とする有向木になる.
これは帰納法で証明可能です.1 ステップ進めるときに,未訪問の点に進むならば明らかです.そうでない場合には,根から有向木内の頂点に向かって辺を張り,その頂点から出る辺を削除するという操作で有向木が保たれます.
「必要条件 1」で求めた列 $(x_v)$ と各頂点の色からこのグラフは作ることができるので,これで「必要条件 2」が得られます.
十分性の証明
必要条件 1, 2 を合わせると十分条件にもなることを示します.
必要条件 1 で各辺を通る回数を求めました.この回数を上限として,問題のルールに沿って可能な限り進みます.必要条件 1 の回数の釣り合いから,終点 $t$ はクエリで与えられた目的地と一致しているはずです.問題となるのは,使われずに余っている辺の有無です.
使われずに余っている辺でグラフを作ると,連結成分ごとに Eulerian になります.辺をひとつ以上含む連結成分について考えます.
未訪問の点だけからなる連結成分
このような点では色の必要条件を満たしているとすると,すべての辺で $2$ 色ともの出る辺が余っています.するとひとつの点からグラフの辺で到達できる点はすべて到達可能,特に $n$ に到達可能となりますが,$n$ の出次数は $0$ なので矛盾です.
訪問済の点を含む連結成分
辺をひとつ以上含む連結成分において,すべての点の入次数・出次数はともに正です.出次数が正であることから,必ず「必要条件 2」で述べた辺は余っています.よってこの連結成分において,「必要条件 2」で述べた辺だけを残すと functional graph ができて特に cycle が出来ます.これは「必要条件 2」に矛盾します.

