概要
問題文 → ■
公式解説 → 存在するか分からず
自分の提出 → ■
色のない状態で非自明な図を書いたりして,全然解けそうにないと思っていたんですが,曲線に色がついていることがめちゃくちゃ重要だった.
部分点解法
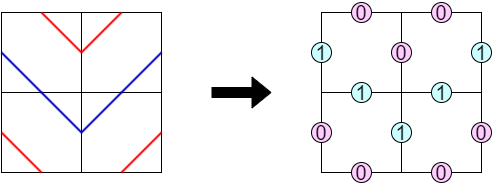
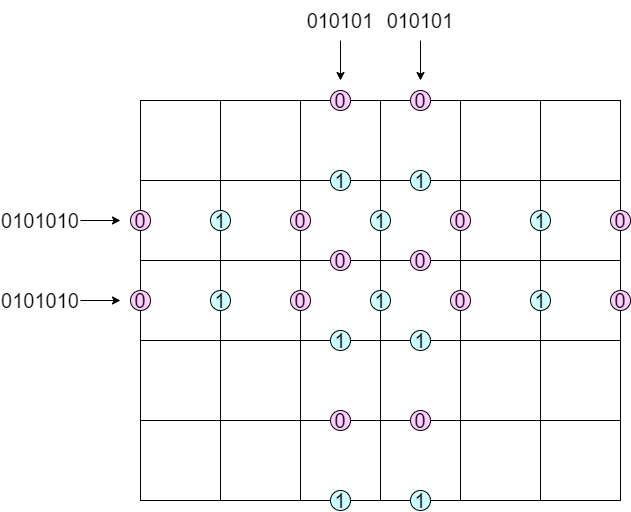
すべての「辺の中点」は,どちらか一方の色の曲線が通ります.そこで,「辺の中点」の色を定義できます.各中点に対して,$0$ または $1$ を割り当てます.
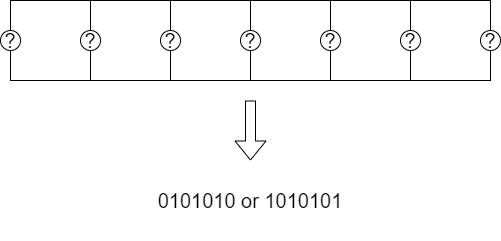
向かい合う中点の色は逆の色になるというのがポイントです.これによって,「各行や各列について,$0101…$ であるか $1010…$ であるかの 2 通りのどちらかを選ぶ方法」であって適切なものを数える問題へと言い換えられます.
定めた 01 列を行のタイプ・列のタイプなどと呼ぶことにします.
次の 4 つに分類して数えましょう.
- (A) どの隣接する行のタイプも異なる.どの隣接する列のタイプも異なる.
- (B) ある隣接する行のタイプが等しい.どの隣接する列のタイプも異なる.
- (C) どの隣接する行のタイプも異なる.ある隣接する列のタイプが等しい.
- (D) ある隣接する行のタイプが等しい.ある隣接する列のタイプが等しい.
(A), (B), (C) はほぼ同じです.
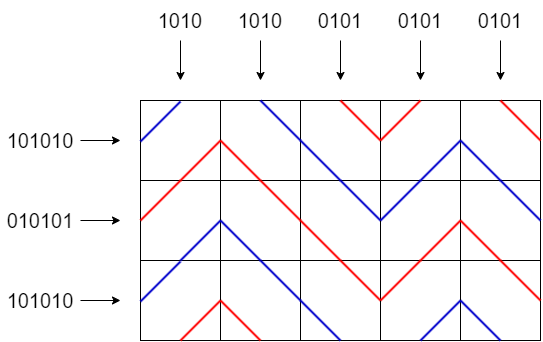
列タイプが交互であるとき,どのようなパターンがありうるかを考えます.列タイプを固定して,各行の 2 タイプの決め方を考えると,どの行をどのタイプとしても条件を満たすことが確認できます.

行のタイプを決めたときの曲線の様子は,平行線が並んでいる形になり,特にすべて上から下の向きにのみ進む線として見ることができるので,サイクルはできません.
したがって列タイプが交互であるようなパターンは $2\cdot 2^W$ 通りあることが分かります.行タイプが交互であるようなパターンも同じで,重複 $4$ 通りを適切にすることで,(A), (B), (C) それぞれを数えることができます.
(D) について考えます.同タイプで隣接する行・列の場所を固定して考えます.
まず,その部分タイプの決め方のうち半数は中央に長さ 4 のサイクルが出来るので不適切です.
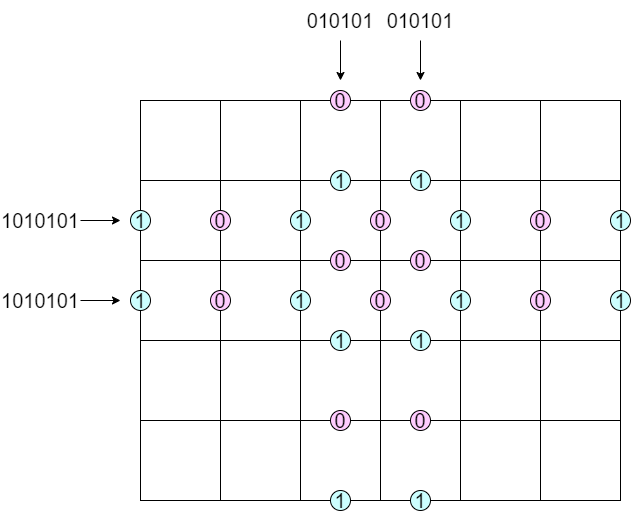
そうでない決め方をすると,ちょうどひとつの配置が条件を満たすことが確認できます.長さ 4 のサイクルができないようにすると,中央から順にすべての行・列のタイプが確定するからです.
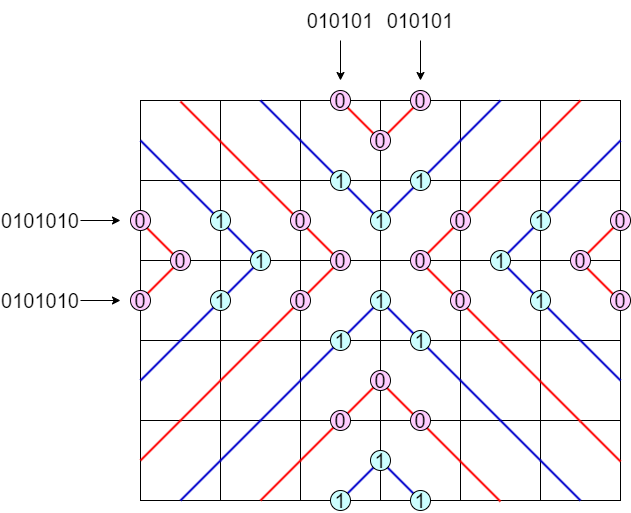
よって (D) タイプは,どの 2 行・2 列のタイプが等しいかを固定するごとに $2$ 通りのパターンがあり,総数は $2(H-1)(W-1)$ 通りです.
満点解法
行タイプ・列タイプという $H+W$ 個のものを適切に決める問題だと考えます.
上で見たように,タイプが交互という条件があって扱いにくいですが,これは奇数インデックスを予め flip しておくという方法をとれば簡潔になります.
適切に変形すると,次に帰着することができます:
- 01 列 A, B を決める問題です.入力では,A[i]=k や B[j]=k という条件が $2N$ 個来ます.数えるべきは,次のいずれかを満たすものです:
- A は定数列で B はそうではない.
- B は定数列で A はそうではない
- A, B ともに定数列である.
- A, B ともに $(x,x,\ldots, x, 1-x, 1-x \ldots)$ の形である.
ここまで整理できれば簡単です.一番難しそうな最後のタイプも,軸ごと独立な数え上げの積として計算できることが分かります.

