| |
A |
B |
C |
D |
E |
F |
| 問題文 |
■ |
■ |
■ |
■ |
■ |
■ |
| 自分の提出 |
■ |
■ |
■ |
■ |
■ |
■ |
| 結果 |
AC |
AC |
AC |
AC |
AC |
AC |
全体感想
52分、2ペナで17位でした。
開始時のいざこざで、遅いスタートでした。リロード連打はお行儀が悪いかなと思い、公式twitterで開始時刻が再定義されるのを待っていたけど、良い戦略ではなかったですね。
DEFとも、かなり難しめだったように感じたので、ちゃんと全完できて嬉しいです。つまらない誤答を出したのが反省。
問題B – Count ABC
部分文字列のカウントは、
の要領でできます。

(出典:https://docs.python.org/ja/3/library/stdtypes.html)
これは厳密には、「部分列として現れる回数」を数えているわけではないことに注意しましょう。

今回の問題では、ある文字が複数の ‘ABC’ に含まれることはありえないので、問題が起きません。
問題C – Count Order
itertools.permutations が、辞書順に順列を生成します。全部の順列を生成したのち、何番目に現れたかを取得しました。
permutations = list(itertools.permutations(range(1, N+1)))
p = permutations.index(P)
q = permutations.index(Q)
問題D – Semi Common Multiple
普通の意味での「公倍数」であれば、2 つずつの数の情報をマージしていける(「6 の倍数かつ 8 の倍数」→「24の倍数」など)ので、同種の方法が適用できるかを考えました。したがって、「数が 2 種のときの「半公倍数」を観察してみよう」と考えました。
「6, 10」だと、「3の奇数倍」「5の奇数倍」となって、これはそのまま最小公倍数に置き換えて「15の奇数倍」が条件となります。例えば、「6, 8」だと、要求が「3の奇数倍」「4の奇数倍」となりますが、これは両立不可能であることなどを発見します。
何か良い観察を見つけたら、なるべくきちんと一般化しておくのが良いです。
(1) $a,b$ の $2$ で割れる回数が異なるとき:両立しない
(2) $a,b$ の $2$ で割れる回数が等しいとき:これらをその最小公倍数に取り換えてよい
ことが分かります。あとはこれを実装すればよいです。最小公倍数はとても大きくなる場合があるので、$M$ を超えた場合には処理を打ち切るなどの対策が必要です(私は $0$ に置き換えて計算を続行する形で実装)。
途中で、
・$a, b$ よりも、 $a/2$, $b/2$ を主体に見た方が考察も実装も易しくなる
ことに気づきました。私は気づいたのは、ほぼ解法が分かった頃でしたが、本当は初手にこれを考えておいた方が良かった気がします。
問題E – Change a Little Bit
これもなかなかの難問です。そもそも記号がごちゃごちゃしていて、読解の時点でわりと難易度があるように思います。
「最小コストの全ての和」を問われているので、まずは「最小コスト」について理解を深めるのが先決です。
最初から揃っている bit をいじる必要はありません。これは、そのような bit をいじる操作があったとき、その bit に対する操作を全て取り消すことで総コストが改善することから分かります。また、これは操作過程についても成り立つので、揃っていない bit をいじる回数もちょうど 1 回だと分かります。結局、「変更位置をそろえる順番」のみが問題です。操作前半から単純に大きな係数がかかるため、
・操作手順 = 異なる bit のうち、コスト最小のものから順に一致させていく
が分かります。
あとは、全部を足し合わせるところです。$C$ を降順にソートしておき、$C_0, C_1, C_2, \ldots$ の寄与回数を数えます。
・$C_k$ の寄与:
「変更位置」が、自身よりコストの高いところにいくつあるかで場合分けします。重み $n$ で寄与するときの、コストに高いところの変更位置の選び方が、$\binom{k}{n-1}$ 通りあります。したがって、\[\sum_{n=1}^{k+1}d\binom{k}{n-1} = \sum_{n=0}^{k}(n+1)\binom{k}{n}\] が計算できればよさそうです。
二項係数の和の式変形をしたい場合は、二項定理に基づきましょう。\[ f(x) = (1+x)^k = \sum_{n=0}^k\binom{k}{n}x^n\] とします。係数ごとに $d+1$ 倍したいです。微分 $\frac{d}{dx}x^{n+1} = dx^n$ を利用すると、\[\frac{d}{dx}(xf(x)) = \sum_{n=0}^k(n+1)\binom{k}{n}x^n\]
が分かるので、$xf(x)$ を微分して $x = 1$ を代入すると求める和が手に入ります。
その他の戦略
(1)確率・期待値の考え方にもとづくと、もっと簡単です。あるコストの重みについては、「コスト大きい側の bit が食い違っているごとに $+1$」です。「重みの期待値」を求めることを考えると、「大きい側の bit ごと」が 1 つあるごとに、重みが $+1/2$ になると分かります。よって、個数ごとに集計する(二項係数の和を処理する)必要はないです。
(2)$N = 3,4,5$ あたりの場合に、各コストの寄与回数を計算してみる(例えばサンプル 3 を愚直実装で計算して、各数値の寄与回数を調べる)と答の予測が立ってしまう問題です。証明なしですがACを狙えます。また、答の予測を立てた上で証明を考えるというアプローチも良いでしょう。
問題F – Xor Shift
うーん、他の方針にも目を奪われそうになってしまうのが少し厄介。
初めに考えたこととして、「$\mathrm{sum}(A)$, $\mathrm{sum}(B)$ を比べると、足すべき数が分かりそうというもの。$N$ が奇数だとこれで良いのですが、$N$ が偶数だとうまくいきませんでした。
もう少し別の不変量を考えます。
・「$a,b,c$」「$a\oplus x, b\oplus x, c\oplus x$」
と書き並べて、不変量を考えます。$a\oplus b = (a\oplus x) \oplus (b \oplus x)$ が見つかりました。
次のような変換を考えます:
・$A = [a_1,a_2,a_3,a_4,a_5] \mapsto [a_1\oplus a_2,a_2\oplus a_3,a_3\oplus a_4,a_4\oplus a_5,a_5\oplus a_1] = f(A)$
全ての項の $\oplus x$ しても、変換の結果は変わりません。また、$f(A)$ と $a_1$ の値から、元の数列 $A$ が復元できます。
したがって、問題から shift を除いた場合には、「$f(A) = f(B)$ であることと作れることが同値。作れるときには、$x = b_1 \oplus a_1$ が唯一の $x$ である」ことが分かります。
あとは、次の問題を解けばよいです:
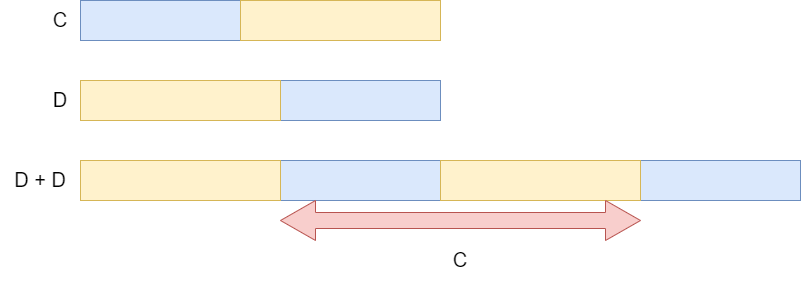
・列 $C = f(A)$, $D = f(B)$ が与えられる。$C$ を巡回シフトさせて、$D$ に一致するのはいつか?
いくつかの方法がありますが、$D$ を2周分持つのが簡単で、周期的な列を扱う際にたまに出てくるテクニックです。$D + D$ から、$C$ を探し出す問題に帰着されます。
これは、文字列アルゴリズムの問題です。解説PDFにある、KMP法のほか、
・ある部分文字列が、Cと完全一致するかを、RollingHash を用いて判定する
・$S = C + D + D$ に対して、Z アルゴリズムを適用して、$S$ との共通接頭辞長が $\mathrm{len}(C)$ 以上になっている接尾辞を検出する
などの方法があります。
変換 $f$ について
xor は、加法の一種なので、 $[a_1 + x, a_2 + x, a_3 + x, \ldots]$ に変換していると思えば、隣接する 2 項の差が不変量になるのは自然でした。