概要
公式解説と同様に,最小費用流をセグメント木を用いて管理するという方針です.公式解説の解説は Hall の定理を経由するなど少しまわりくどいように感じられ,また辺の削除に対応していないため計算量が悪化しています.
本解説ではまず最小費用流の差分更新について整理し,公式解説では扱われていない辺の削除についても追加とほぼ同様に考えられることを確認します.それを踏まえて本問題が計算量 $O((N+Q)\log (N+Q))$ 時間で解けることを確認します.
最小費用(循環)流による定式化
まずクエリを無視します.
本問題は明らかに最大重みマッチングとして定式化できます(仕事・日付をマッチさせる).最大重みマッチングは最小費用流により解けます.適当に辺の個数を減らすと,大体次のようなネットワークの最小費用流を求める問題になります.
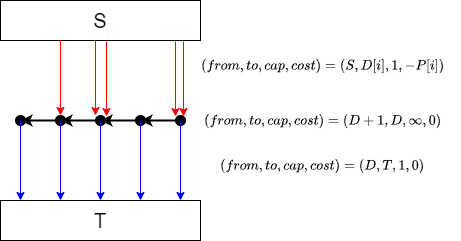
クエリも含めて考えると,赤い辺を追加したり削除したりしながら最小費用流を求める問題を解けということになります.
以下記述を簡単にするため,さらに $T$ から $S$ に容量 $\infty$,コスト $0$ の辺を追加しておきます.すると,求めるべきは最小費用循環流ということになります.
差分更新(一般論)
本記事ではフローについて,容量や流量の整数性を仮定します.(なお容量が整数であれば,流量が整数であるような最適解が存在しますし,通常のアルゴリズムはそのような解を出力します).
ネットワーク $G$ のフロー $f$ に対して残余グラフ $G_f$ が定義されます.この定義は省略するので知らない場合は別の文献でフローのさらに基本的なことを勉強してください.
まずフローの閉路分解についても確認しておきます.なおこの記事では(通常のように)閉路やパスと言えば同じ頂点を 1 度しか通らないやつです.
(循環流の閉路分解)循環流はいくつかの閉路の和である.
流量の総和が $0$ になるまで閉路を引いていく感じで簡単に証明できます.流入量と流出量が等しいことから,流れている辺に従って適当に進んでいけばどこかに閉路ができます.
循環流ではなく $S$ から $T$ へのフローという定式化の場合には,「$ST$ パスと閉路の和」というように言い換えてください.このような記述を簡潔にするためにこの記事では循環流による定式化を選択しましたが,これらは互いにすぐに変換可能です.これは記事の以下の部分の多くの部分についても同様に当てはまります.
以下ではあるアルゴリズムの出力が最小費用循環流の最適解であることを示す議論を行います.そのためには次が便利です:
(最適性の確認方法)フロー $f$ が最小費用循環流であることは,残余グラフ $G_f$ に負閉路が存在しないことと同値である.
これは,あるフローと他のフローの差分が残余グラフにおける循環流,したがって閉路の和として書けることから分かります.(循環流ではなく $S$ から $T$ へのフローという定式化をする場合には,「負閉路または重み負の ST パス」とします.)
この事実から,最小循環費用流を得るには,残余グラフにおいて負閉路が存在する限り流し続けるというアルゴリズムが得られます.以下ではネットワークを容量 $1$ だけ変化させた場合には,負閉路に流す操作高々 $1$ 回で最適解を更新できることを示します.
辺の追加
最小費用循環流の最適解 $f$ が得られているとして,残余グラフを $G_f$ としたとき,容量 $1$ の辺 $e$ をひとつ追加したときの最適解について考えます.これは次により得られます:
(辺 $e$ の追加)$G_f+e$ において $e$ を含む負閉路であってコスト最小のものをとり,その負閉路に沿って $1$ 流す.そのような負閉路がなければ何もしない.
まず $G_f+e$ に $e$ を含む負閉路が存在しないとしましょう.追加前に最適解を得ているという仮定のもとでは $G_f$ に負閉路は存在しないので,結局 $G_f+e$ には負閉路が存在しないことが分かります.よって残余グラフに負閉路が存在しないので $e$ の追加後にも $f$ は最適解になっています.
$G_f+e$ においてコスト最小の負閉路 $C$ が存在したとします.$f+C$の残余グラフに負閉路がないことを示しましょう.$f+C$ の残余グラフに負閉路 $C’$ があったとして,それらの和 $C+C’$ を考えます.これは $G_f+e$ における循環流なので,$G_f+e$ における閉路の和で書けます.
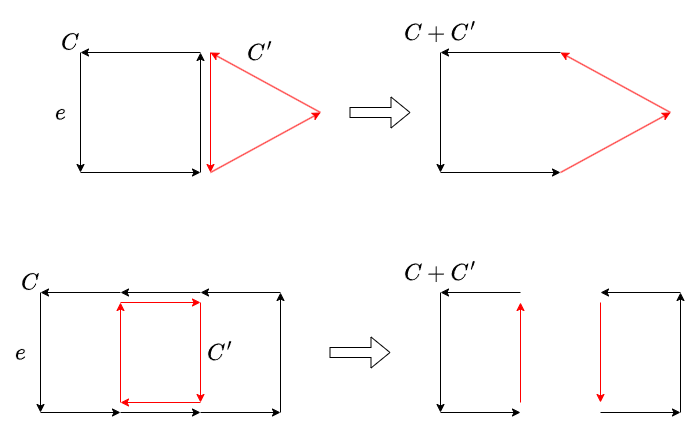
このうち $e$ を通らないものの重みは $G_f$ の最適性より非負なので,これらを引けば,$G_f+e$ の閉路であって重みが $C$ の重み未満であるものがとれます.これは $C$ がコスト最小であったことに矛盾します.
辺の削除
最小費用循環流の最適解 $f$ が得られているとして,残余グラフを $G_f$ としたとき,容量 $1$ の辺 $e$ をひとつ削除したときの最適解について考えます.これは次により得られます:
(辺 $e$ の削除)$f$ において $e$ が流量 $0$ ならば,$f$ がそのまま $G-e$ の最小費用循環流となる.流量 $1$ ならば,$G_f$ において $e$ の逆辺を含む閉路(これは必ず存在する)であってコスト最小のものをとり,その閉路に沿って $1$ 流す.
辺の削除によって最適解が改善することは明らかにありえないので,流量 $0$ の場合は明らかです.流量 $1$ の場合を考えます.まず $e$ の逆辺を含む閉路が存在することは,フローの閉路分解から分かります.そのようなコスト最小の閉路 $C$ に沿って流したあとに $e$ を含まない負閉路 $C’$ が存在したとすると,$C+C’$ を考えれば,辺の追加の場合と同様に $C$ のコスト最小の仮定に矛盾します.
本問の解法
$S$ と数直線の間に辺がない状態からはじめて,追加や削除をしながら最小費用流を管理します.
各時点で,フローの情報は次によって表されます.
- $S$ 側の辺の流量(それぞれ $0$ または $1$)
- $T$ 側の辺の流量(それぞれ $0$ または $1$)
- 数直線上の辺の流量(それぞれ非負整数)
なお数直線上の辺の流量はその他の辺の流量から一意に定まりますが,このことを意識する必要はありません.
あくまでフロー,つまり流量の組を管理することに気を付けてください.例えば具体的なマッチング(フローのパス・閉路分解)の情報は管理しません.最悪計算量を悪くしないままマッチングの差分更新を陽に行うことは,変更箇所が多くなってしまうので不可能でしょう.
辺の追加
辺の追加については,その辺を通る最小コストの負閉路を探すのでした.循環流の設定を $ST$ フローの設定に戻せば,残余グラフにおける次の 2 種を探すことになります.
- $S$ から $e$ を通り $S$ に戻る閉路
- $S$ から $e$ を通り $T$ に至るパス
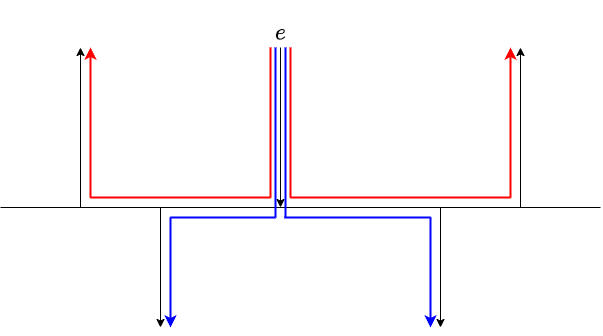
数直線上の辺はコスト $0$ なので,$S,T$ との間の辺で最適なものをひとつ選ぶということになります.選べる辺はどのようなものでしょうか?
残余グラフ上での辺の向きが適切でなければいけないので,$S$ 側の流量 $1$ の辺や $T$ 側の流量 $0$ の辺が対象です.それだけではなく,残余グラフ上で数直線上での辺がなければいけません.左方向には容量 $\infty$ の辺があるのでどこにでも行けます.右方向には流量が正の辺をさかのぼることしかできません.
数直線上の流量の列をセグメント木で管理することにすると,右側にどこまで進めるかは,区間 min のできるセグメント木の max_right() で求まります.フローを流した場合の流量の列の更新は区間加算です.なお流量をその差分の prefix sum と見なすことで,遅延セグメント木ではなくセグメント木で実装することも可能です.
なお,$S$ 側の辺の逆辺は重み正なので,パスを作れるならばパス,そうでないならばサイクルを作ることになります.
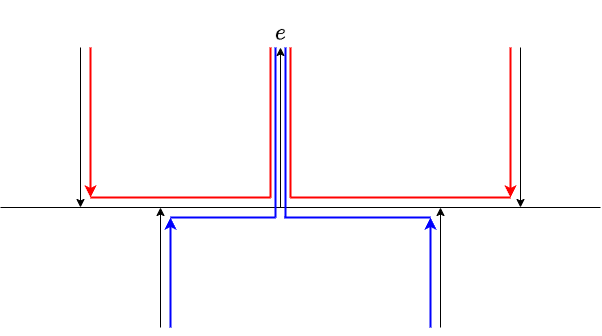
辺の削除
辺 $e$ の流量が $0$ ならば簡単です.流量 $1$ の場合には,残余グラフにおいて $e$ の逆辺を通る最小重みの閉路を探すのでした.これもほとんど同じです.
解答例

関連
最小費用流の差分更新を利用すると,partially retroactive priority queue を実装することもできます.priority queue に対する push(x), pop_max() という操作列の最終結果は本問と同様の最大重みマッチングとして記述できるので,ほとんど同じです.
partially retroactive priority queue とは何であるかは noshi91さんによるユーザー解説 を参照してください.Library Checker にも足したいと思っています(issue).
本解法を fully retroactive priority queue (時刻 $t$ で pop される要素も答える)の実装に利用するのは難しいと思います.

